近期看到一张梗图,有的学生将自由基引发剂偶氮二异丁腈(AIBN)看成了铝硼氮(AlBN),让人忍俊不禁。与此同时,这不禁让人好奇,形如AlBN的物质是否存在、是什么结构。作为固体的AlBN并非是空穴来风(取成语习惯意义)。AlN具有纤维锌矿结构,是一种半导体物质,而AlBN可以看作AlN中部分B取代Al和N的产物。
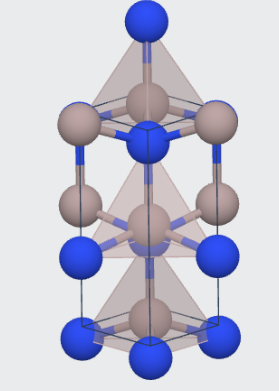
(AlN的晶体结构图片来自Materials Project)
在1993年,Shiro等人提出B可能可以嵌入AlN、GaN等半导体中(Japanese journal of applied physics, 1993, 32(10R): 4413.)起到带隙调控作用。次年,Shin等通过三乙基硼、三甲基铝和氨气的高温气相化学沉积生长出了包含Al、B、N的薄膜,只不过B的含量不能超过1%,否则会导致分别生成AlN和BN。陆续又有人报道了其他合成的尝试(Applied Physics Letters, 2007, 91(4).、Applied Physics Letters, 2024, 125(7).等),都只能做到2%以下的含B量。这种AlBN薄膜具有铁电性能(Applied Physics Letters, 2024, 125(7).)。
接下来,我们探讨AlBN作为分子又如何。显然,这种分子应该高度不稳定,需要在气相下制备,通过基质分离等手段表征。这篇文章顺便作为一个教学,展示如何使用量子化学工具研究AlBN的+1离子的性质;同时起到抛砖引玉的作用,如果有朋友对这个体系感兴趣可以对电中性、-1电荷等体系进行研究。
使用Gaussian 16在M06-2X/def2-TZVP水平下进行构型优化(这个分子很小,很适合使用CCSD或多参考态方法优化。但为了简单起见,也为了顺便作为对更多人有意义的教学,这里采用了DFT)。只考虑包含Al-B-N顺序连接的分子,也就是排除诸如线性的Al-N-B等可能性。
AlBN分子是个很简单的例子,因为结构只可能有三种:直线型、V型和环状。对于更多原子的团簇,想要知道是什么结构,必须进行构型搜索,可以利用ABCluster、molclus等工具。尽管人们可以尝试写出它的路易斯结构式,但很难预计AlBN+的电子结构究竟如何、是不是双自由基或多自由基。由于V型可以当作线性分子的衍生型,我们首先分别建立直线型和环状的初始结构,假定它是个单重态,进行波函数稳定性检查:
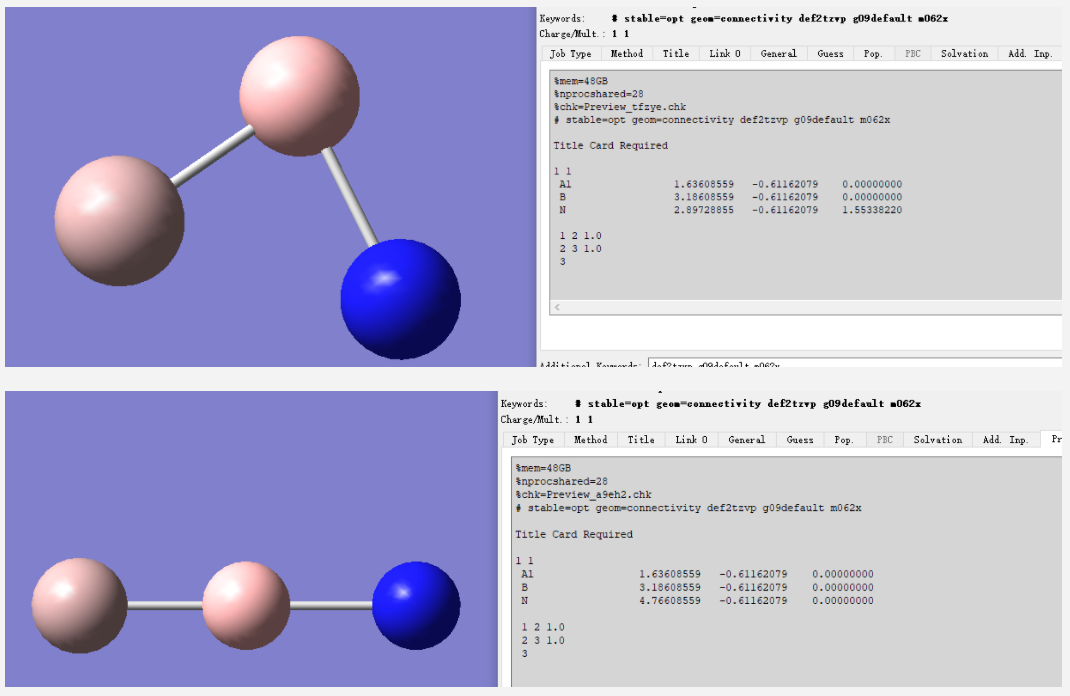
对于单重态,如果不特殊指定,量化程序将默认电子完全配对,得到闭壳层结果。然而若该分子是多自由基,只是总自旋恰好抵消,则闭壳层结果显然是错误的。即使手动指定开壳层计算(如写um062x),两种自旋电子的地位仍然会保持相同,最终得到与闭壳层完全相同的结果。这相当于是给波函数施加了“在闭壳层子空间内寻找能量最低点”的限制,而在完整的参数空间里找到的则是能量的鞍点,这称作具有“波函数不稳定性”(instability of wavefunction)。
在这一步中,通过stable=opt关键字和(r)m062x,首先进行闭壳层计算,随后检查波函数稳定性。如果发现波函数稳定,则结束运算;否则找到一个稳定的波函数。最终得到的稳定波函数中,两种电子与其他电子的相互作用不再像闭壳层那样完全相同,能够正确反映双自由基特征,这又称作对称性破缺计算(BS-calculation, broken symmetry calculation)。
结果发现,环状的单重态波函数稳定,而线性结构的单重态为开壳层。这可以通过查找输出文件里的SCF Done次数直观看到。在环状结构中,初次RM06-2X计算就得到了稳定波函数,而对于线性结构,RM06-2X得到的波函数不稳定,接下来尝试寻找了一个UM06-2X波函数,依然不稳定,最终找到的第三个UM06-2X波函数是稳定的,能量比一开始低了0.034 a.u..
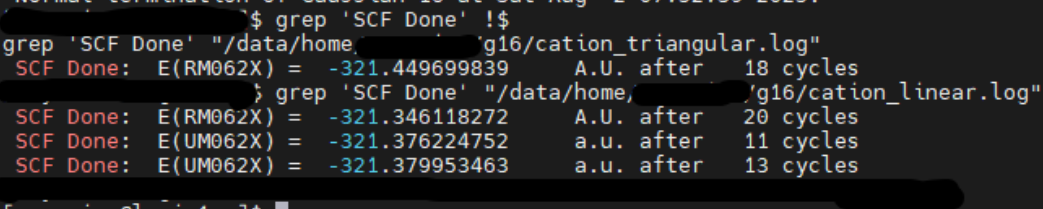
这些稳定波函数储存在chk文件里。接下来通过guess=read读取稳定波函数,进行构型优化和频率计算(stable=opt不能与opt freq联用)。
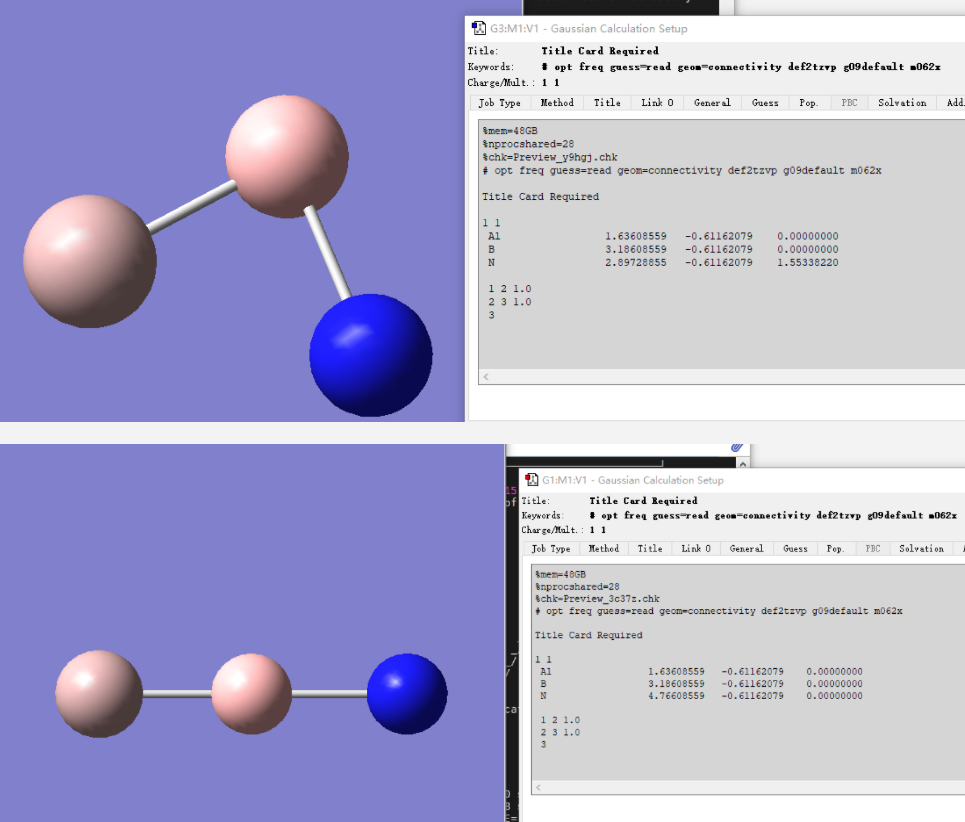
经过构型优化,发现线性AlBN+稍微弯曲,键角为173.2°,B-N和B-Al键长分别为1.301和2.108 angstrom。而环状AlBN+则近似直角三角形,B-N, N-Al, B-Al距离为1.483, 1.756, 2.069 angstrom。
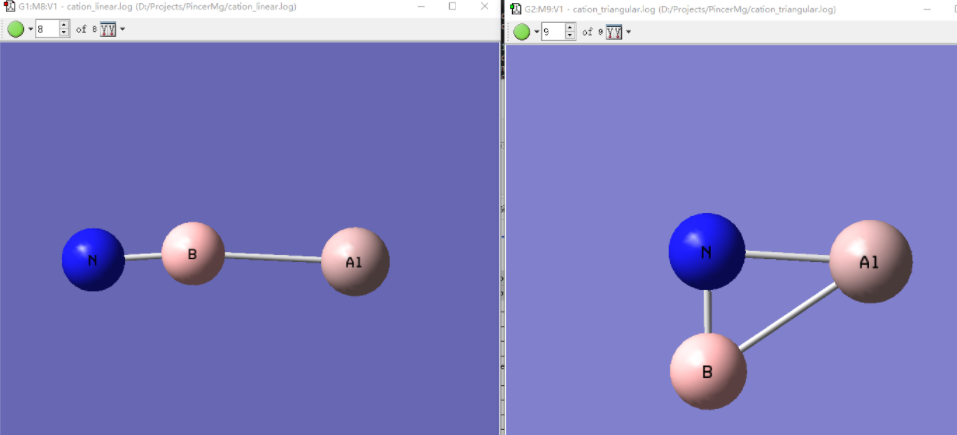
优化完成后,线性AlBN+仍然是开壳层单重态分子。开壳层单重态提示三重态能量很可能与单重态接近,因此我们还要去尝试三重态。
三重态分子变成了完全的线性。观察两个分子的自旋布居,发现两者电子结构很不一样。对于单重态分子,单电子分布在Al和N上;而对于三重态分子,2个单电子平均分布在3个原子上。对于线性分子,三重态是基态,在298 K下的自由能比开壳层单重态低3.2 kcal/mol。而环状结构能量更低,比三重态的线性结构低28.7 kcal/mol。
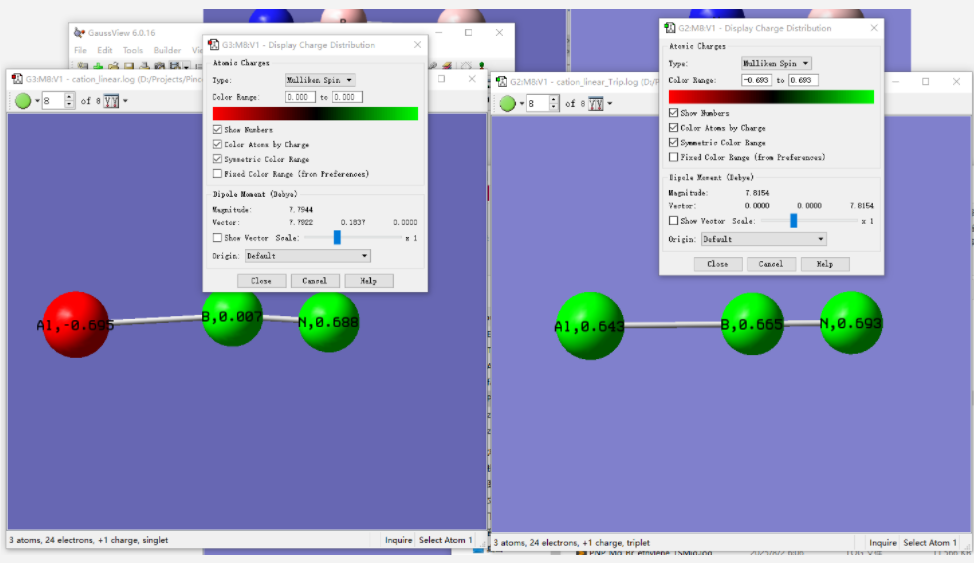
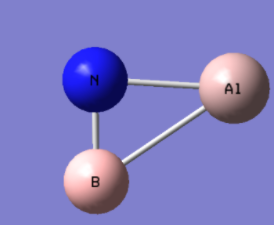
既然已经知道了AlBN+的基态是三角结构,接下来让我们尝试弄清楚其中的成键方式。
使用Multiwfn载入fchk文件,依次按9键级分析、1Mayer键级,立刻得到三根键的键级:
Bond orders with absolute value >= 0.050000
# 1: 1(Al) 2(B ) 1.16880058
# 2: 1(Al) 3(N ) 1.20225113
# 3: 2(B ) 3(N ) 2.01351415
根据这个键级,很容易推断出它比较接近如下共振式:
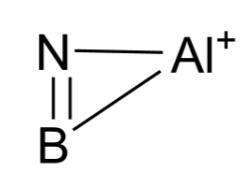
然而,需要小心的是,键级为1.2虽然接近1,但不代表就只形成一根单键;键级为2同理。由于键能是连续的,键级也是连续的谱系;当人们说存在几根键时,指的是存在几组重要的轨道相互作用,它们每个可能都只贡献零点几个键级。对于AlBN+分子到底是怎么样呢?我们可以通过其他角度辅助分析。回到Multiwfn主界面,进入主功能19轨道定域化,选择1定域化占据轨道,这样可以将分子轨道定域到容易与共振结构对应的成键轨道上去。其中轨道1-12为占据轨道,1-7是内核轨道,而8-12是双原子之间的成键轨道。对照这几个成键轨道的轨道成分和形状,可以进行分类:
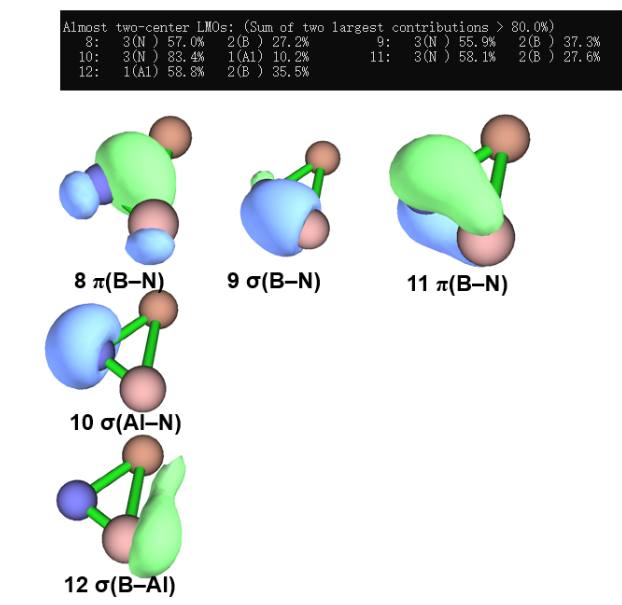
首先需要注意,定域化轨道的能量需要单独计算,当前轨道顺序不严格反映轨道能量。另外轨道形状不总能完全反映轨道组成。例如轨道10,乍看起来像是N上的孤对电子,但其实有10%的Al原子轨道成分 ,其实对应一根σ(Al-N)键,只不过两者电负性差距太大,导致成键轨道中N占据了主导。通过定域化轨道分析,我们发现B-N键虽然Mayer键级整体为2,但其实有3组成键作用。此外,这个分子的LUMO轨道也主要集中在B-N附近而不是Al的空轨道处。因此,这个分子更适合用如下共振式描述:
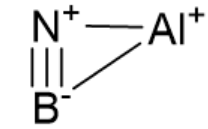
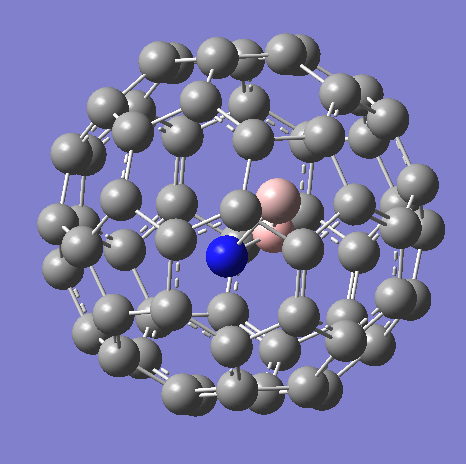
最后,虽然AlBN及相关分子显然不容易在通常条件下稳定存在,但将它们封装进富勒烯或碳纳米管是可能的,这也是研究这类分子的常见策略。以下是M06-2X/6-31G(d)水平下得到的AlBN+@C60结构,这个离子整体位于C60球体中心,内壁碳原子稳定了配位不饱和的Al原子,距离在2 angstrom左右: